너무나도 어렵군... 화이팅... 🔥
20168번: 골목 대장 호석 - 기능성
첫 줄에 교차로 개수 N, 골목 개수 M, 시작 교차로 번호 A, 도착 교차로 번호 B, 가진 돈 C 가 공백으로 구분되어 주어진다. 이어서 M 개의 줄에 걸쳐서 각 골목이 잇는 교차로 2개의 번호와, 골목의
www.acmicpc.net
20182번: 골목 대장 호석 - 효율성 1
첫 줄에 교차로 개수 N, 골목 개수 M, 시작 교차로 번호 A, 도착 교차로 번호 B, 가진 돈 C 가 공백으로 구분되어 주어진다. 이어서 M 개의 줄에 걸쳐서 각 골목이 잇는 교차로 2개의 번호와, 골목의
www.acmicpc.net
20183번: 골목 대장 호석 - 효율성 2
첫 줄에 교차로 개수 N, 골목 개수 M, 시작 교차로 번호 A, 도착 교차로 번호 B, 가진 돈 C 가 공백으로 구분되어 주어진다. 이어서 M 개의 줄에 걸쳐서 각 골목이 잇는 교차로 2개의 번호와, 골목의
www.acmicpc.net
문제
소싯적 호석이는 골목 대장의 삶을 살았다. 호석이가 살던 마을은 N 개의 교차로와 M 개의 골목이 있었다. 교차로의 번호는 1번부터 N 번까지로 표현한다. 골목은 서로 다른 두 교차로를 양방향으로 이어주며 임의의 두 교차로를 잇는 골목은 최대 한 개만 존재한다. 분신술을 쓰는 호석이는 모든 골목에 자신의 분신을 두었고, 골목마다 통과하는 사람에게 수금할 것이다. 수금하는 요금은 골목마다 다를 수 있다.
당신은 A 번 교차로에서 B 번 교차로까지 C 원을 가지고 가려고 한다. 호석이의 횡포를 보며 짜증은 나지만, 분신술을 이겨낼 방법이 없어서 돈을 내고 가려고 한다. 하지만 이왕 지나갈 거면, 최소한의 수치심을 받고 싶다. 당신이 받는 수치심은 경로 상에서 가장 많이 낸 돈에 비례하기 때문에, 결국 갈 수 있는 다양한 방법들 중에서 최소한의 수치심을 받으려고 한다. 즉, 한 골목에서 내야 하는 최대 요금을 최소화하는 것이다.
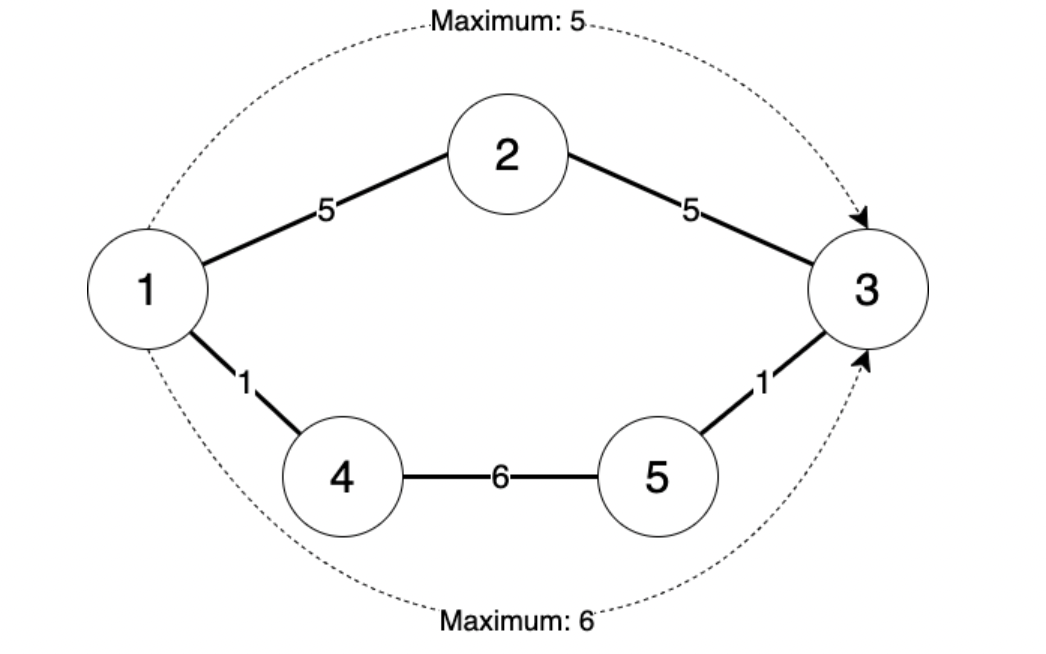
예를 들어, 위의 그림과 같이 5개의 교차로와 5개의 골목이 있으며, 당신이 1번 교차로에서 3번 교차로로 가고 싶은 상황이라고 하자. 만약 10원을 들고 출발한다면 2가지 경로로 갈 수 있다. 1번 -> 2번 -> 3번 교차로로 이동하게 되면 총 10원이 필요하고 이 과정에서 최대 수금액을 5원이었고, 1번 -> 4번 -> 5번 -> 3번 교차로로 이동하게 되면 총 8원이 필요하며 최대 수금액은 6원이 된다. 최소한의 수치심을 얻는 경로는 최대 수금액이 5인 경로이다. 하지만 만약 8원밖에 없다면, 전자의 경로는 갈 수 없기 때문에 최대 수금액이 6원인 경로로 가야 하는 것이 최선이다.
당신은 앞선 예제를 통해서, 수치심을 줄이고 싶을 수록 같거나 더 많은 돈이 필요하고, 수치심을 더 받는 것을 감수하면 같거나 더 적은 돈이 필요하게 된다는 것을 알게 되었다. 마을의 지도와 골목마다 존재하는 호석이가 수금하는 금액을 안다면, 당신이 한 골목에서 내야하는 최대 요금의 최솟값을 계산하자. 만약 지금 가진 돈으로는 절대로 목표 지점을 갈 수 없다면 -1 을 출력하라.
입력
첫 줄에 교차로 개수 N, 골목 개수 M, 시작 교차로 번호 A, 도착 교차로 번호 B, 가진 돈 C 가 공백으로 구분되어 주어진다. 이어서 M 개의 줄에 걸쳐서 각 골목이 잇는 교차로 2개의 번호와, 골목의 수금액이 공백으로 구분되어 주어진다. 같은 교차로를 잇는 골목은 최대 한 번만 주어지며, 골목은 양방향이다.
출력
호석이가 지키고 있는 골목들을 통해서 시작 교차로에서 도착 교차로까지 C 원 이하로 가는 경로들 중에, 지나는 골목의 요금의 최댓값의 최솟값을 출력하라. 만약 갈 수 없다면 -1을 출력한다.
20168과 20182, 20183번은 문제가 같다. 다른점은 주어진 변수의 입력 범위이다.



20168번은 N의수가 최대 10까지이다. 따라서 모든 교차로를 확인할 경우 최대 O(n^2)의 복잡도를 가지는데 이는 100이므로 시간초과 범위 내에서 해결이 가능하다.
반면 20182번은 N의 수가 최대 100,000까지여서 O(n^2)의 경우 100,000,000,000 이 되므로 5초 제한에서 timeout이 발생한다. 따라서 20182번과 20183번은 탐색의 수를 줄여야 한다.
20168 : DFS 로 풀기
앞선 문제는 연산횟수가 최대 100이므로 DFS로 풀어보았다.
import sys
input = sys.stdin.readline
n, m, a, b, c = map(int, input().split())
road = [[] for _ in range(n+1)] # index가 교차로 (n+1), 이어지는골목과 비용을 append 한다
for _ in range(m):
from_c, to_c, cost = map(int, input().split())
# 양방향 골목이므로 두번 삽입
road[from_c].append((to_c, cost))
road[to_c].append((from_c, cost))
res_max_min = sys.maxsize
def dfs(from_city, total_cost, max_cost):
global res_max_min
# 경로의 총 비용이 소지한 비용을 넘어서면 return
if total_cost > c:
return
# 위의 validation을 통과하고, 도착지점에 도착하면 값 갱신
if from_city == b:
res_max_min = min(res_max_min, max_cost)
return
# 비용미초과, 도착지점 미도달 상태라면 계속해서 탐색
for to_city, to_cost in road[from_city]):
# 이전에 방문하지 않은 교차로만 탐색
if not visit[to_city]:
visit[from_city] = True
dfs(to_city, total_cost+to_cost, max(max_cost, to_cost))
visit[from_city] = False
visit = [False] * (n+1)
visit[0] = True
visit[a] = True
dfs(a, 0, 0)
if res_max_min == sys.maxsize:
res_max_min = -1
print(res_max_min)해당 풀이로 20168번 풀이가 가능하다.
20182, 20183 : 이분탐색과 다익스트라 알고리즘 활용하기
정답에서 요구하는 것은 "최소값이 정답이 되는 것" 이다. 이러한 유형의 문제에서는 "이분탐색" 으로 정답이 되는 값을 탐색하며 풀 수 있다. 참고로 이분탐색법은 값이 정렬되어 있을때 O(logN)의 시간복잡도를 지닌다.
이분탐색법으로 정답이 되는값 "목표 교차로까지 가는 경로중 최대 비용들 중에서의 최소값" 을 탐색하며, 해당 값으로 도착지점까지 도달할 수 있는지 다익스트라 알고리즘으로 탐색한다.
모든 골목의 비용 리스트 = costs
이분탐색으로 탐색한 값 = mid
이분탐색으로 탐색한 값 기준 제한 골목 비용 = costs[mid]
한개 경로의 최대값 one_max
모든 경로의 one_max 들 중에서의 최소값 = road_max_min
교차로 = 노드
골목 = 간선
다익스트라 알고리즘은 a에서 b까지 가는 경로의 최단거리를 찾아낸다. 즉 시작지점에서 도착지점까지 최소비용을 찾아내고, 그 값이 costs[mid] 값과 같거나 그 값보다 적다면 해당 그 값이 답이 될수 있다는 뜻이다.
반면, 최단거리 탐색 중 한개 간선의 비용이 mid값 보다 크다면 해당 조건으로 탐색은 불가능한 것이므로 mid 값을 키워주며 탐색한다.
import heapq
import sys
sys.stdin = open("input.txt")
n, m, a, b, c = map(int, input().split())
costs = []
road = [[] for _ in range(n + 2)]
for _ in range(m):
from_cc, to_cc, ccost = map(int, input().split())
costs.append(ccost)
road[from_cc].append((to_cc, ccost))
road[to_cc].append((from_cc, ccost))
def check_cost(mid):
distances = [sys.maxsize for _ in range(n + 1)]
distances[a] = 0
edge = []
heapq.heappush(edge, [0, a]) # 비용과 현재 노드
while edge:
this_cost, this_node = heapq.heappop(edge)
# 최단경로 확인한다 : 이미 이번 노드로 가는 비용이 누적 비용보다 적다면 갱신 X
if distances[this_node] < this_cost:
continue
for next_node, next_cost in road[this_node]:
if distances[next_node] > this_cost + next_cost and next_cost <= mid:
distances[next_node] = next_cost + this_cost
heapq.heappush(edge, [this_cost + next_cost, next_node])
if distances[b] > c:
return False
return True
road_max_min = sys.maxsize
costs.sort()
lt = 0
rt = len(costs) -1
while lt <= rt:
mid = (lt + rt) // 2
# mid 값을 최대로 갖는 경로가 있는지 확인한다.
check_res = check_cost(costs[mid])
if check_res:
# 있다면 최대 값을 더 줄여본다
rt = mid -1
# 답으로 기록한다.
road_max_min = min(road_max_min, costs[mid])
else:
# 없다면 최대값을 더 늘려본다
lt = mid +1
if road_max_min == sys.maxsize:
print(-1)
else:
print(road_max_min)이때 check_cost 함수 내에서 목표골목 b까지의 최단거리가 완성되었을때 그 값이 c 보다 크다면 결국엔 갈수 없는 경로이므로 mid 값을 줄여준다.
위 풀이로 20182과 20183 모두 해결 가능하다.
Python으로 풀었을 경우 백준에서는 Python3 와 Pypy3 두가지로 채점 가능하다.
Python3로 채점했을때 시간초과가 뜬 경우 Pypy3로 채점하면 통과하기도 하는데 위 문제중 20182가 그러한 경우이다. 따라서 Pypy3 로 제출하면 된다!

'풀이로그' 카테고리의 다른 글
| [백준] 11403 python 플로이드 워셜, deque 풀이와 시간복잡도 비교하기 (0) | 2024.03.10 |
|---|---|
| [백준] 2630 python : 분할정복 알고리즘 활용하기 (쿼드 트리) (0) | 2024.03.06 |
| [백준] 2792 Python | 15810 Python : 이분탐색법 (0) | 2024.03.03 |
| [알고리즘] 백준 | 배열 돌리기 Python (16926, 16927) (2) | 2024.02.14 |
| [Java] 코딩테스트 값 입력받는 방법 : Scanner, next(), nextInt(), nextLine() (0) | 2024.02.02 |








